1. Комплексный чертеж в прямоугольных проекциях
Начертательная геометрия - раздел геометрии, научные основы которого были разработаны французским математиком и физиком Г. Монжем для решения задач, связанных с определением размеров, форм и положения в пространстве линий, поверхностей, тел и их пересечений, при помощи построения их изображений на плоскости. Свойства геометрических фигур исследуются по их ортогональным проекциям, как правило, на три взаимно перпендикулярные плоскости, а геометрические построения в пространстве заменяются более доступными геометрическими построениями на соответствующих проекциях [9].
Чертежи должны быть по возможности наглядными, обратимыми, т.е. давать возможность точно воспроизводить форму и размеры предмета, обладать простотой построения. Черчение является интернациональным графическим языком, а грамматикой этого языка является начертательная геометрия [10].
Для отображения объектов на чертеже ставится задача определить проекции точек объекта на заданную плоскость. Существуют различные способы проецирования (центральное, косоугольное и прямоугольное (ортогональное)) и в зависимости от положения центров проецирования и плоскостей проекций могут быть получены различные проекционно-изобразительные системы. Наиболее распространенной системой является система прямоугольных (ортогональных) проекций, или метод Монжа.
Совокупность двух или более взаимосвязанных ортогональных проекций геометрической фигуры называется комплексным чертежом. Метод комплексного чертежа в прямоугольных проекциях называется методом Монжа [4].
Суть способа ортогонального проецирования заключается в том, что через каждую точку геометрической фигуры проводится проецирующая прямая, перпендикулярная плоскости проекций, и точка пересечения ее с этой плоскостью принимается за ортогональную проекцию точки.
В методе Монжа плоскости проекций П1 и П2 взаимно перпендикулярны, а центры проецирования удалены в бесконечность по направлениям, перпендикулярным к плоскостям проекций.
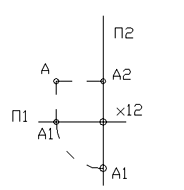
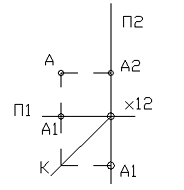
На рис. 1 плоскости проекций показаны сбоку по направлению их линии пересечения x12. Как видно из рисунка, неограниченные плоскости проекций П1 и П2 делят пространство на четыре четверти, показанные римскими цифрами. Для того, чтобы проекции точки получить на одной плоскости (плоскости чертежа), достаточно горизонтальную плоскость проекций П1 совместить с фронтальной плоскостью проекций П2 вращением вокруг линии их пересечения x12, или провести биссекторную плоскость К между П1 и П2, точку проецировать на эту плоскость в вертикальном направлении, а затем перепроецировать на фронтальную плоскость П1 (рис.2) [4].
Начертательная геометрия - раздел геометрии, научные основы которого были разработаны французским математиком и физиком Г. Монжем для решения задач, связанных с определением размеров, форм и положения в пространстве линий, поверхностей, тел и их пересечений, при помощи построения их изображений на плоскости. Свойства геометрических фигур исследуются по их ортогональным проекциям, как правило, на три взаимно перпендикулярные плоскости, а геометрические построения в пространстве заменяются более доступными геометрическими построениями на соответствующих проекциях [9].
Чертежи должны быть по возможности наглядными, обратимыми, т.е. давать возможность точно воспроизводить форму и размеры предмета, обладать простотой построения. Черчение является интернациональным графическим языком, а грамматикой этого языка является начертательная геометрия [10].
Для отображения объектов на чертеже ставится задача определить проекции точек объекта на заданную плоскость. Существуют различные способы проецирования (центральное, косоугольное и прямоугольное (ортогональное)) и в зависимости от положения центров проецирования и плоскостей проекций могут быть получены различные проекционно-изобразительные системы. Наиболее распространенной системой является система прямоугольных (ортогональных) проекций, или метод Монжа.
Совокупность двух или более взаимосвязанных ортогональных проекций геометрической фигуры называется комплексным чертежом. Метод комплексного чертежа в прямоугольных проекциях называется методом Монжа [4].
Суть способа ортогонального проецирования заключается в том, что через каждую точку геометрической фигуры проводится проецирующая прямая, перпендикулярная плоскости проекций, и точка пересечения ее с этой плоскостью принимается за ортогональную проекцию точки.
В методе Монжа плоскости проекций П1 и П2 взаимно перпендикулярны, а центры проецирования удалены в бесконечность по направлениям, перпендикулярным к плоскостям проекций.
На рис. 1 плоскости проекций показаны сбоку по направлению их линии пересечения x12. Как видно из рисунка, неограниченные плоскости проекций П1 и П2 делят пространство на четыре четверти, показанные римскими цифрами. Для того, чтобы проекции точки получить на одной плоскости (плоскости чертежа), достаточно горизонтальную плоскость проекций П1 совместить с фронтальной плоскостью проекций П2 вращением вокруг линии их пересечения x12, или провести биссекторную плоскость К между П1 и П2, точку проецировать на эту плоскость в вертикальном направлении, а затем перепроецировать на фронтальную плоскость П1 (рис.2) [4].

Рисунок 1 - Плоскости проекций
а) |
б) |
Рисунок 2 - Получение проекций точки на одной плоскости чертежа
а) совмещением П1 с П2 вращением вокруг линии их пересечения x12;
б) проецирование с помощью биссекторной плоскости К между П1 и П2
Для отображения вида сбоку (профильная проекция) проецирование осуществляется на третью плоскость, перпендикулярную П1 и П2 , обозначаемую П3.
Введем некоторые понятия.
Изображение, получаемое при совмещении плоскостей проекций, называется "эпюр" [5].
Прямой уровня называется прямая, параллельная какой-либо одной плоскости проекций. Горизонталь - прямая, параллельная П1. Фронталь - прямая, параллельная П2. Профиаль - прямая, параллельная П3.
Проецирующие прямые - это такие прямые, которые перпендикулярны какой-либо одной плоскости проекций. Горизонтально-проецирующая прямая - прямая, перпендикулярная плоскости П1. Фронтально-проецирующая прямая - прямая, перпендикулярная плоскости П2. Профильно-проецирующая прямая - прямая, перпендикулярная плоскости П3.
Плоскости частного положения - это плоскости уровня и плоскости проецирующие. Плоскость уровня - это плоскость, параллельная одной из плоскостей проекций. Проецирующая плоскость - это плоскость, перпендикулярная какой-либо одной плоскости проекций. В зависимости от того, какой плоскости она перпендикулярна, ее называют фронтально- проецирующей, горизонтально- проецирующей и профильно-проецирующей.
К свойствам ортогонального проецирования относятся:
Проекция точки - есть точка.
Проекция прямой - прямая в общем случае.
Если точка принадлежит прямой, то проекция точки принадлежит проекции прямой (следствие: для построения проекции прямой, достаточно построить проекции двух принадлежащих ей точек).
Проекции параллельных прямых параллельны.
Точка пересечения линий проецируется в точку пересечения их проекций.
Проекция геометрической фигуры не меняется при параллельном переносе плоскостей проекций.
Если геометрическая фигура параллельна какой-либо плоскости проекции, то проекция фигуры конгруэнтна самой фигуре [10].
2. Виды задач начертательной геометрии
Решение многих задач способами начертательной геометрии, в конечном счете, сводится к определению позиционных и метрических характеристик геометрических объектов. В связи с этим все многообразие задач может быть отнесено к двум группам:
Задачи позиционные - решение, которых должно давать ответ на вопрос о взаимном расположении геометрических объектов (в частном случае, выяснить их взаимную принадлежность) как по отношению друг к другу, так и относительно системы координатных плоскостей проекций.
Задачи метрические - при решении задач этой группы появляется возможность ответить на вопросы, касающиеся как внутренней метрики заданных геометрических объектов (определение расстояния между различными точками объекта и нахождения углов между линиями и поверхностями, принадлежащими этому объекту), так и определение расстояний между точками и величин углов между линиями и поверхностями, принадлежащими различным объектам.
В начертательной геометрии задачи решаются графически. Количество и характер геометрических построений при этом определяются не только сложностью задачи, но и в значительной степени зависит от того, с какими проекциями (удобными или неудобными) приходится иметь дело. При этом наиболее выгодным частным положением геометрического объекта следует считать:
- положение, перпендикулярное к плоскости проекций (для решения позиционных, а в ряде случаев, и метрических задач);
- положение, параллельное по отношению к плоскости проекций (при решении метрических задач).
При решении метрических задач, связанных с определением истинных размеров изображенных на эпюре фигур, могут встретиться значительные трудности, если заданные проекции не подвергнуть специальным преобразованиям [8].
3. Преобразование чертежа
Для упрощения решения метрических и позиционных задач инженерной графики применяются различные методы преобразования ортогональных проекций. После таких преобразований новые проекции позволяют решать задачу минимальными графическими средствами.
Методы преобразования основываются, как правило, на двух принципах:
1) изменение взаимного положения объекта проецирования и плоскостей проекций;
2) изменение направления проецирования.
Первый принцип может быть реализован путем выбора новых плоскостей проекций при неподвижном положении объекта проецирования (метод замены плоскостей проекций) или перемещением объекта в новое положение относительно неподвижных плоскостей проекций (метод плоскопараллельного перемещения и метод вращения вокруг различных осей). Отмеченные методы используются в основном для решения метрических задач.
Метод преобразования проекций, основанный на изменении направления проецирования относительно неизменных плоскостей проекций (косоугольное вспомогательное проецирование), используется преимущественно для решения позиционных задач.
Существует еще ряд методов преобразования проекций, которые подробно рассматриваются в специальной литературе по начертательной геометрии [4].
Рассмотрим метод замены плоскостей проекций и метод вращения вокруг линии уровня.
3.1 Замена плоскостей проекций
Метод замены плоскостей проекции основан на преобразовании проекций с помощью замены основных плоскостей проекций новыми, которые выбираются так, чтобы объект проецирования или его элементы изобразились на них в удобном для решения положении. При этом должно сохраниться ортогональное проецирование на взаимно перпендикулярные плоскости. Для решения той или иной задачи необходимо заменять одну, либо обе плоскости проекций.
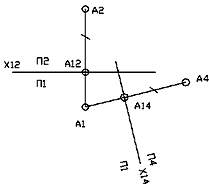
Пусть задана система взаимно перпендикулярных плоскостей проекций П2/П1, точка А и ее проекции - в этой системе (А1; А2). Пусть фронтальная плоскость проекции П2 заменена новой фронтальной плоскостью проекций П4 (новые фронтальные плоскости проекций обычно обозначают четным цифровым индексом: П4; П6 и т. д., а горизонтальные - нечетным: П5; П7 и т.д. (плоскость П3 - профильная плоскость проекций). Плоскость П4 проведена под произвольным углом к плоскости П2, но обязательно под прямым углом к плоскости проекций П1. Горизонтальный след этой плоскости представляет собой новую ось проекций х14. Таким образом, от системы плоскостей проекций П2/П1 мы перешли к системе П4/П1. Ортогонально спроецируем точку А на новую плоскость проекций П4 и получим новую фронтальную проекцию А4 точки А. Расстояние от новой проекции точки до новой оси (А4А14) равно расстоянию от замененной (старой) проекции точки до старой оси (А2А12), т. е. А4А14 = А2А12. Это и является инвариантом метода замены плоскостей проекции. В новой системе плоскостей проекций П4/П1 получим пару проекций А1 и А4, которые также однозначно определяют положение точки А в пространстве.
Для получения комплексного чертежа новой системы плоскостей проекций плоскость П4 вращением вокруг оси х14 совмещаем с плоскостью П1. Тогда проекции А1 и А4 будут принадлежать линии связи, перпендикулярной к оси х14. Расстояние от А4 до оси х14 равно расстоянию от А2 до оси х12 (рис. 3).
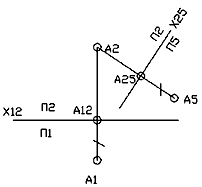
При замене горизонтальной плоскости проекций П1 на новую плоскость П5 получаем новую проекцию точки А5. И здесь расстояние от новой проекции А5 до новой оси х25 (А5А25) равно расстоянию от заменяемой проекции А1 до старой оси х12 (А1А12): А1А12 = А5А25. Комплексный чертеж новой системы получим, совместив плоскость П5 вращением вокруг оси х25 с плоскостью проекций П2. Проекции точки А2 и А5 также располагаются на линии связи, перпендикулярной к оси х25 (рис. 4), а расстояние от А5 до оси х25 равно расстоянию от А1 до оси х12.
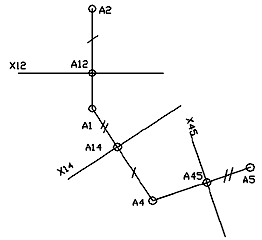
Замена двух плоскостей проекций выполняется последовательно: сначала заменяется одна плоскость (П2/П1 = П4/П1 или П2/П1 = П2/П5), а затем в промежуточной системе вторая плоскость заданной системы (П4/П1= П4/П5 или П2/П5 = П4/П5). При второй замене (рис. 5) плоскости проекций расстояние от новой проекции А5 точки А до новой оси х45 (А5А45) также равно расстоянию от заменяемой проекции А1 до промежуточной (старой) оси х14 : А5А45 = А1А14 [4].
Введем некоторые понятия.
Изображение, получаемое при совмещении плоскостей проекций, называется "эпюр" [5].
Прямой уровня называется прямая, параллельная какой-либо одной плоскости проекций. Горизонталь - прямая, параллельная П1. Фронталь - прямая, параллельная П2. Профиаль - прямая, параллельная П3.
Проецирующие прямые - это такие прямые, которые перпендикулярны какой-либо одной плоскости проекций. Горизонтально-проецирующая прямая - прямая, перпендикулярная плоскости П1. Фронтально-проецирующая прямая - прямая, перпендикулярная плоскости П2. Профильно-проецирующая прямая - прямая, перпендикулярная плоскости П3.
Плоскости частного положения - это плоскости уровня и плоскости проецирующие. Плоскость уровня - это плоскость, параллельная одной из плоскостей проекций. Проецирующая плоскость - это плоскость, перпендикулярная какой-либо одной плоскости проекций. В зависимости от того, какой плоскости она перпендикулярна, ее называют фронтально- проецирующей, горизонтально- проецирующей и профильно-проецирующей.
К свойствам ортогонального проецирования относятся:
Проекция точки - есть точка.
Проекция прямой - прямая в общем случае.
Если точка принадлежит прямой, то проекция точки принадлежит проекции прямой (следствие: для построения проекции прямой, достаточно построить проекции двух принадлежащих ей точек).
Проекции параллельных прямых параллельны.
Точка пересечения линий проецируется в точку пересечения их проекций.
Проекция геометрической фигуры не меняется при параллельном переносе плоскостей проекций.
Если геометрическая фигура параллельна какой-либо плоскости проекции, то проекция фигуры конгруэнтна самой фигуре [10].
2. Виды задач начертательной геометрии
Решение многих задач способами начертательной геометрии, в конечном счете, сводится к определению позиционных и метрических характеристик геометрических объектов. В связи с этим все многообразие задач может быть отнесено к двум группам:
Задачи позиционные - решение, которых должно давать ответ на вопрос о взаимном расположении геометрических объектов (в частном случае, выяснить их взаимную принадлежность) как по отношению друг к другу, так и относительно системы координатных плоскостей проекций.
Задачи метрические - при решении задач этой группы появляется возможность ответить на вопросы, касающиеся как внутренней метрики заданных геометрических объектов (определение расстояния между различными точками объекта и нахождения углов между линиями и поверхностями, принадлежащими этому объекту), так и определение расстояний между точками и величин углов между линиями и поверхностями, принадлежащими различным объектам.
В начертательной геометрии задачи решаются графически. Количество и характер геометрических построений при этом определяются не только сложностью задачи, но и в значительной степени зависит от того, с какими проекциями (удобными или неудобными) приходится иметь дело. При этом наиболее выгодным частным положением геометрического объекта следует считать:
- положение, перпендикулярное к плоскости проекций (для решения позиционных, а в ряде случаев, и метрических задач);
- положение, параллельное по отношению к плоскости проекций (при решении метрических задач).
При решении метрических задач, связанных с определением истинных размеров изображенных на эпюре фигур, могут встретиться значительные трудности, если заданные проекции не подвергнуть специальным преобразованиям [8].
3. Преобразование чертежа
Для упрощения решения метрических и позиционных задач инженерной графики применяются различные методы преобразования ортогональных проекций. После таких преобразований новые проекции позволяют решать задачу минимальными графическими средствами.
Методы преобразования основываются, как правило, на двух принципах:
1) изменение взаимного положения объекта проецирования и плоскостей проекций;
2) изменение направления проецирования.
Первый принцип может быть реализован путем выбора новых плоскостей проекций при неподвижном положении объекта проецирования (метод замены плоскостей проекций) или перемещением объекта в новое положение относительно неподвижных плоскостей проекций (метод плоскопараллельного перемещения и метод вращения вокруг различных осей). Отмеченные методы используются в основном для решения метрических задач.
Метод преобразования проекций, основанный на изменении направления проецирования относительно неизменных плоскостей проекций (косоугольное вспомогательное проецирование), используется преимущественно для решения позиционных задач.
Существует еще ряд методов преобразования проекций, которые подробно рассматриваются в специальной литературе по начертательной геометрии [4].
Рассмотрим метод замены плоскостей проекций и метод вращения вокруг линии уровня.
3.1 Замена плоскостей проекций
Метод замены плоскостей проекции основан на преобразовании проекций с помощью замены основных плоскостей проекций новыми, которые выбираются так, чтобы объект проецирования или его элементы изобразились на них в удобном для решения положении. При этом должно сохраниться ортогональное проецирование на взаимно перпендикулярные плоскости. Для решения той или иной задачи необходимо заменять одну, либо обе плоскости проекций.
Пусть задана система взаимно перпендикулярных плоскостей проекций П2/П1, точка А и ее проекции - в этой системе (А1; А2). Пусть фронтальная плоскость проекции П2 заменена новой фронтальной плоскостью проекций П4 (новые фронтальные плоскости проекций обычно обозначают четным цифровым индексом: П4; П6 и т. д., а горизонтальные - нечетным: П5; П7 и т.д. (плоскость П3 - профильная плоскость проекций). Плоскость П4 проведена под произвольным углом к плоскости П2, но обязательно под прямым углом к плоскости проекций П1. Горизонтальный след этой плоскости представляет собой новую ось проекций х14. Таким образом, от системы плоскостей проекций П2/П1 мы перешли к системе П4/П1. Ортогонально спроецируем точку А на новую плоскость проекций П4 и получим новую фронтальную проекцию А4 точки А. Расстояние от новой проекции точки до новой оси (А4А14) равно расстоянию от замененной (старой) проекции точки до старой оси (А2А12), т. е. А4А14 = А2А12. Это и является инвариантом метода замены плоскостей проекции. В новой системе плоскостей проекций П4/П1 получим пару проекций А1 и А4, которые также однозначно определяют положение точки А в пространстве.
Для получения комплексного чертежа новой системы плоскостей проекций плоскость П4 вращением вокруг оси х14 совмещаем с плоскостью П1. Тогда проекции А1 и А4 будут принадлежать линии связи, перпендикулярной к оси х14. Расстояние от А4 до оси х14 равно расстоянию от А2 до оси х12 (рис. 3).
При замене горизонтальной плоскости проекций П1 на новую плоскость П5 получаем новую проекцию точки А5. И здесь расстояние от новой проекции А5 до новой оси х25 (А5А25) равно расстоянию от заменяемой проекции А1 до старой оси х12 (А1А12): А1А12 = А5А25. Комплексный чертеж новой системы получим, совместив плоскость П5 вращением вокруг оси х25 с плоскостью проекций П2. Проекции точки А2 и А5 также располагаются на линии связи, перпендикулярной к оси х25 (рис. 4), а расстояние от А5 до оси х25 равно расстоянию от А1 до оси х12.
Замена двух плоскостей проекций выполняется последовательно: сначала заменяется одна плоскость (П2/П1 = П4/П1 или П2/П1 = П2/П5), а затем в промежуточной системе вторая плоскость заданной системы (П4/П1= П4/П5 или П2/П5 = П4/П5). При второй замене (рис. 5) плоскости проекций расстояние от новой проекции А5 точки А до новой оси х45 (А5А45) также равно расстоянию от заменяемой проекции А1 до промежуточной (старой) оси х14 : А5А45 = А1А14 [4].
Рисунок 3 - Замена фронтальной плоскости проекций |
Рисунок 4 - Замена горизонтальной плоскости проекций |
Рисунок 5 - Замена плоскостей проекций |
3.2 Вращение вокруг линий уровня
Рассмотрим метод преобразования комплексного чертежа вращением вокруг линии уровня, который, в частности, может быть применим для решения метрической задачи нахождения натуральной величины треугольника.
Если вращать плоскость общего положения вокруг ее горизонтали или фронтали, то можно добиться, чтобы плоскость стала соответственно горизонтальной или фронтальной. При вращении вокруг горизонтали h (рис. 6) точка А описывает окружность, плоскость которой перпендикулярна к оси вращения h. Горизонтальная проекция траектории вращения точки изобразится прямой, проходящей через горизонтальную проекцию А1 точки, перпендикулярной к горизонтальной проекции горизонтали h1. Горизонтальная проекция центра вращения точки изобразится точкой О1. Отрезок А1О1 - это горизонтальная проекция радиуса вращения точки А. Точка А после поворота окажется лежащей в одной горизонтальной плоскости с горизонталью h, если радиус ее вращения на горизонтальной плоскости проекций изобразится в натуральную величину. Натуральная величина радиуса вращения АО определена способом прямоугольного треугольника как гипотенуза прямоугольного треугольника, один катет которого - отрезок А1О1, а второй равен разности координат концов z отрезка AO (zA - z0). Если от точки O1 на проекции траектории вращения точки А отложить в одну или другую сторону от проекции горизонтали натуральную величину радиуса вращения точки А, получим новую повернутую проекцию А11.
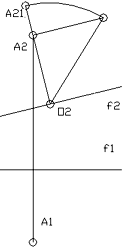
Если осью вращения будет фронталь f, то при вращении точка А описывает окружность, фронтальная проекция которой изобразится прямой, перпендикулярной к f2 (рис. 7). Определив натуральную величину радиуса вращения способом прямоугольного треугольника (O2A2 - величина одного катета, а разность координат (уА - у0) концов отрезка - величина второго), и отложив эту величину по одну и другую сторону f2 , получим повернутое положение А21 точки А [4].
Рассмотрим метод преобразования комплексного чертежа вращением вокруг линии уровня, который, в частности, может быть применим для решения метрической задачи нахождения натуральной величины треугольника.
Если вращать плоскость общего положения вокруг ее горизонтали или фронтали, то можно добиться, чтобы плоскость стала соответственно горизонтальной или фронтальной. При вращении вокруг горизонтали h (рис. 6) точка А описывает окружность, плоскость которой перпендикулярна к оси вращения h. Горизонтальная проекция траектории вращения точки изобразится прямой, проходящей через горизонтальную проекцию А1 точки, перпендикулярной к горизонтальной проекции горизонтали h1. Горизонтальная проекция центра вращения точки изобразится точкой О1. Отрезок А1О1 - это горизонтальная проекция радиуса вращения точки А. Точка А после поворота окажется лежащей в одной горизонтальной плоскости с горизонталью h, если радиус ее вращения на горизонтальной плоскости проекций изобразится в натуральную величину. Натуральная величина радиуса вращения АО определена способом прямоугольного треугольника как гипотенуза прямоугольного треугольника, один катет которого - отрезок А1О1, а второй равен разности координат концов z отрезка AO (zA - z0). Если от точки O1 на проекции траектории вращения точки А отложить в одну или другую сторону от проекции горизонтали натуральную величину радиуса вращения точки А, получим новую повернутую проекцию А11.
Если осью вращения будет фронталь f, то при вращении точка А описывает окружность, фронтальная проекция которой изобразится прямой, перпендикулярной к f2 (рис. 7). Определив натуральную величину радиуса вращения способом прямоугольного треугольника (O2A2 - величина одного катета, а разность координат (уА - у0) концов отрезка - величина второго), и отложив эту величину по одну и другую сторону f2 , получим повернутое положение А21 точки А [4].
Рисунок 6 - Вращение вокруг горизонтали |
Рисунок 7 - Вращение вокруг фронтали |