Алгоритмы автоматического решения задач начертательной геометрии

Существуют различные виды и методы решения задач начертательной геометрии. Создание универсального алгоритма автоматического решения различных видов задач усложняется разнообразием подходов к решению, вариантов конкретных методов, необходимостью учитывать частные случаи расположения геометрических фигур в пространстве. Для решения же задач начертательной геометрии в системе AutoCAD существует множество инструментов, с помощью которых можно решить поставленную задачу начертательной геометрии выбранным методом. Ход построений, производимых пользователем, является, как правило, уникальным (выбор команд, применяемая их последовательность, особенности построений выбранного метода).
Поэтому задача исследования в рамках темы магистерской работы сводится к поиску и классификации общих моментов в алгоритмах автоматического решения задач.
Следует отметить, что преподавателями и студентами многих вузов создаются электронные учебники [8, 10], электронные задачники [15], а также обучающе-контролирующие программные комплексы по курсу начертательной геометрии. В подобных разработках контроль знаний осуществляется в виде тестов "вопрос-ответ", теоретический материал по курсу представлен статическими рисунками, а также с помощью мультимедиа средств.
Отметим, что описание функций модулей программного комплекса для постановки и решения задач по начертательной геометрии [18], разработанного в МИФИ (Россия), в общем похоже на функции разрабатываемого автором продукта, однако данный комплекс был выполнен на языке Turbo Pascal в операционной среде DOS, что не соответствует современным требованиям к ПО.
Однако решения задачи в постановке, аналогичной теме данной магистерской работы, при поиске в Интернет встречено не было. Преимуществом разрабатываемого продукта является то, что обучение проходит в той же среде - в среде AutoCAD, в которой требуется от студентов выполнение лабораторных работ. Контроль знаний предполагает проверку практического решения конкретной задачи. При этом преподавателю нет необходимости самостоятельно проверять точность построений, поскольку это сделает программа и выдаст результат.
При разработке алгоритмов и реализации системы обучения предусматриваются следующие элементы:
Визуализация исходной задачи.
При этом осуществляется ввод начала системы координат и исходных данных, проверка корректности ввода. Производится прорисовка осей координат и вывод соответствующих исходных данных в виде эпюра (фронтальная и горизонтальная проекция геометрических фигур).
Предложение пользователю решить задачу самостоятельно.
Возможность пошаговой демонстрации геометрических построений для решения поставленной задачи, в ходе которой пользователь самостоятельно изучает ход построений. Демонстрация осуществляется по этапам с паузами и комментариями, выводимыми при построениях. После завершения построений могут быть выведены результаты (например, искомые координаты, длины, углы).
Установлено, что графика, предъявленная в динамике, понимается и запоминается на 30-40% лучше, чем предъявленная в статике, и ЭВМ позволяет использовать это преимущество динамической графики в интерактивном режиме. Этап материального действия должен постоянно сопровождаться ознакомлением с действием [13]. В связи с этим пошаговая демонстрация геометрических построений с комментариями облегчает понимание и запоминание.
Алгоритм демонстрации решения задачи может предусматривать запрос точки нового начала системы координат, отличной от введенной при вводе исходных данных задачи. Это удобно, так как построения не будут проводиться многократно на одном месте, кроме того, пользователь может параллельно отслеживать построения, проводимые вызванной функцией, и анализировать собственные построения.
Тестирование. Запрос ответа пользователя и сравнение полученного программой в скрытой форме ответа с предложенным вариантом ответа пользователя, вывод результата и сообщение о том, верный ли ответ получил пользователь.

Дальнейшее исследование и разработки будут направлены на реализацию автоматического решения некоторых метрических задач методом замены плоскостей проекций.
При разработке алгоритмов решения задач начертательной геометрии интересно также предусмотреть возможность предварительной экспертной оценки задачи, подсказки пользователю элементов ее решения на отдельных этапах.
Кроме того, планируется реализовать 3D-демонстрацию решения задач для повышения понимания решения задач с помощью пространственного представления построений.
На данный момент реализован алгоритм решения задачи нахождения натуральной величины треугольника методом вращения вокруг линии уровня.

Пример реализации решения задачи нахождения натуральной величины треугольника методом вращения вокруг горизонтали
Исходные данные задачи: А (18,30,5), В (10,10,12), С (15,15,20).
Демонстрация решения приведена на рис. 1 - 7. Анимация построения приведена на рис. 8.

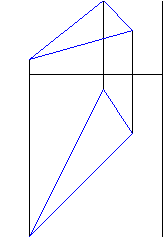
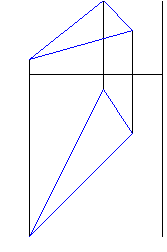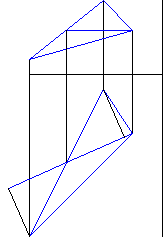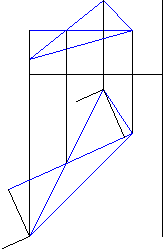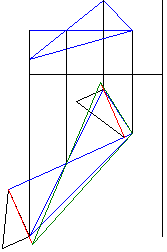
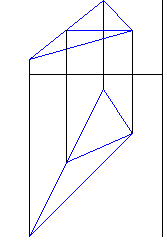
Рисунок 1 - Фронтальная и горизонтальная проекции треугольника	Рисунок 2 - Построение фронтальной и горизонтальной проекции горизонтали треугольника
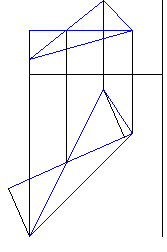
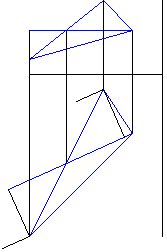
Рисунок 3 - Построение перпендикуляров к фронтальной и горизонтальной проекции горизонтали треугольника, опущенных из проекций вершин треугольника (кроме "средней")	Рисунок 4 - Построение отрезков длинами перпендикуляров, опущенных из фронтальных проекций двух вершин треугольника (кроме "средней") к фронтальной проекции горизонтали, параллельно горизонтальной проекции горизонтали из соответствующих горизонтальных проекций точек "
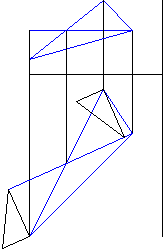
Рисунок 5 - Построение радиусов вращения вершин треугольника в натуральную величину	Рисунок 6 - Построение повернутых вокруг горизонтали проекций вершин треугольника
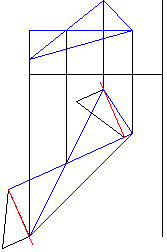
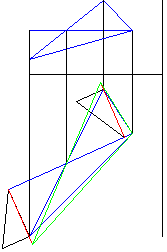
Рисунок 7 - Построение натуральной величины сторон треугольника	Рисунок 8 - Анимация построения натуральной величины треугольника (рис. 1-7)